以下の前記事では統計的仮説検定のコアコンセプトを紹介しました。本記事では統計的仮説検定の弱点や注意点について紹介します。

2 つのエラー
統計的仮説検定を使えば必ず正しい結論が得られるかというともちろんそういうわけではありません。仮説が正しいのに棄却してしまったり、反対に仮説が正しくないのに棄却できなかったりします。前者の間違いを α エラーと呼び、後者を β エラーと呼びます。
これらのエラーを無くすことはできませんが、ある程度コントロールすることはできます。
α エラー
α エラーとは、本当は仮説が正しいのに間違って棄却してしまうことです。さて、α エラーが生じる確率はいくらでしょうか?これは有意水準そのものです。どんなときに仮説が棄却されるのかを思い出しましょう。
仮説が正しいという仮定下において手元のデータが十分珍しいものであるとき、仮説は棄却されるのでした。珍しいというのは、有意水準を下回る確率でしか得られないことを指します。
つまり仮説が正しいという仮定下において、有意水準を下回る確率でしか得られないような珍しいデータが得られた場合、仮説を棄却します。したがって、仮説が正しい場合に仮説を棄却する確率が有意水準だということですね。
有意水準は自分で決めることができますから、α エラーを引き起こすリスクは自由にコントロールできることになります。
β エラー
β エラーは反対に、仮説が正しくないのに棄却できない間違いのことです。β エラーを引き起こす確率は、真の値 (前記事 のコインの例で言えば、表の出る本当の確率) に依存します。ただし以下のような性質を持ちます。
- 仮説と真実の差が大きければ β エラーのリスクは小さくなる。
- これは次の節でも説明しますが、仮説と真実の乖離が大きければ、仮説は棄却されやすくなり、β エラーを引き起こす確率も小さくなります。
- 有意水準を低くすると β エラーのリスクは大きくなる。
- α エラーのリスクを抑えるために有意水準を下げると、β エラーのリスクを増大させることになります。
- つまり α エラーと β エラーはトレードオフの関係にあるということです。
- サンプルサイズを大きくすれば β エラーのリスクは小さくなる。
- サンプルサイズとはデータ量のことでした。
- 有意水準を固定しつつ、β エラーのリスクを一定以下に抑えるには、これくらいのサンプルサイズが必要だ、というサンプルサイズ設計という理論体系もあります。
仮説と真実に乖離があれば有意になりやすい
ここで用語の整理をしておきましょう。以下はすべて同じ意味でしたね。
- p 値が有意水準を下回る
- 結果が有意である
- 仮説が棄却される
仮説としては「コインの表の出る確率は 1/2 である」を使います。以下の 3 パターンのシナリオを考えた場合、下のほうがより仮説が棄却されやすいであろうことは想像がつきますよね。
- 表の出る真の確率は実は 0.51
- 表の出る真の確率は実は 0.6
- 表の出る真の確率は実は 0.9
これを計算で示してみましょう。
有意水準を 5% に設定し、コインを投げる回数は 100 回にしましょう。前回見たように、表の出る回数が 39 回以下もしくは 61 回以上であれば、仮説は棄却されることになります。
真の表の出る確率が 0.51、0.6、0.9 である場合に、それぞれ棄却域に入る確率は以下のグラフのグレーアウトした部分の合計です。
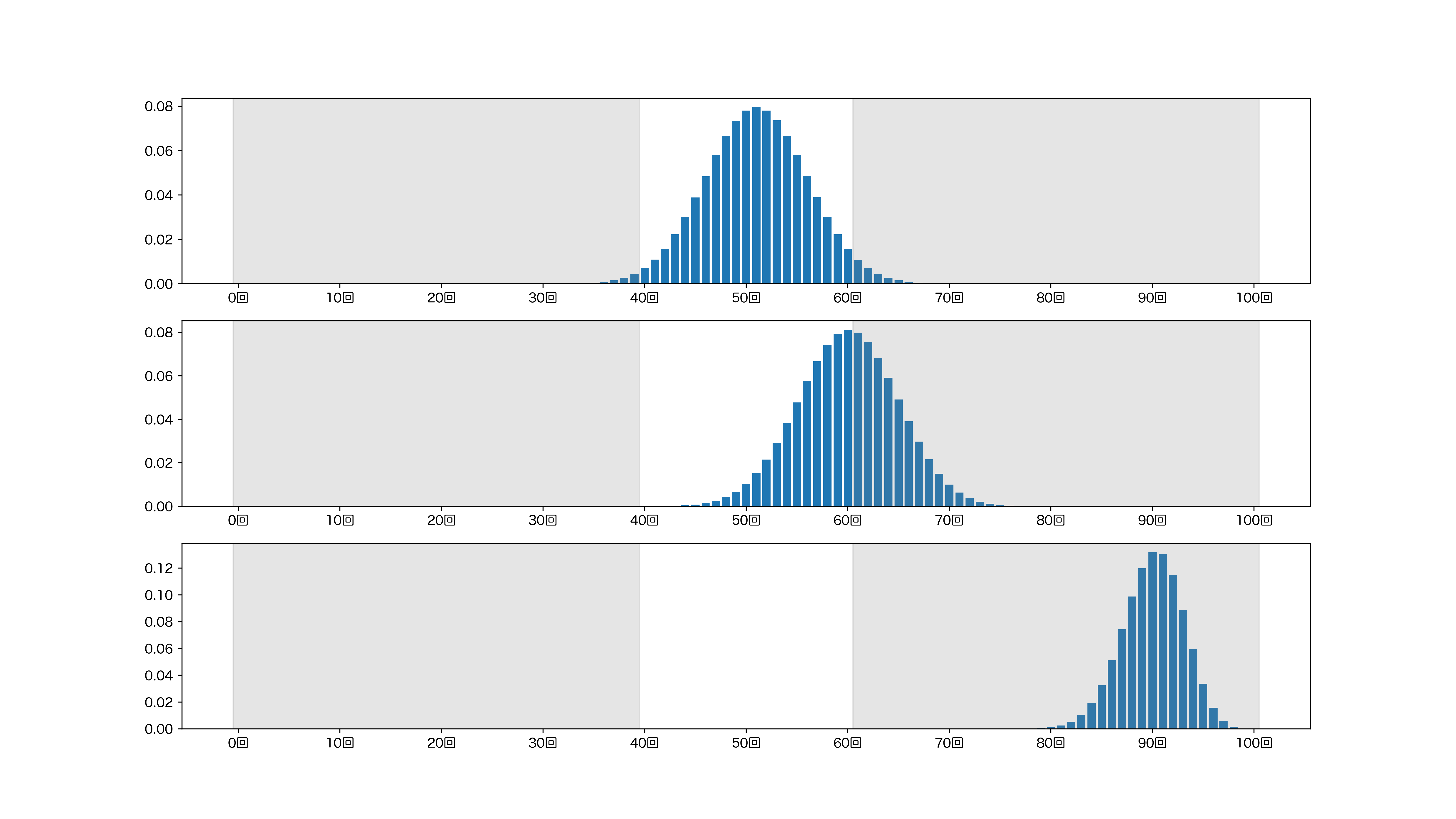
具体的に計算するとこの表のようになります。
| 真の表の出る確率 | 棄却される確率 |
|---|---|
| 0.51 | 0.03886132396202924 |
| 0.6 | 0.46209338234839525 |
| 0.9 | 0.999999999999997 |
ここで計算した値は p 値とは異なるものであることには注意してください。p 値は仮説に基づいて計算される値です。ここでは仮説ではなく真の値に基づいて計算しています。
上の表から、真の表の出る確率が 0.9 である場合、100 回コインを投げて検定を行うと、ほとんど 100% の確率で仮説が棄却されることがわかります。真の表の出る確率が 0.6 である場合、仮説が棄却される確率は 46% 程度ですね。真の表の出る確率が 0.51 である場合は、めったに棄却できないようです。
このように、仮説 (表の出る確率は 1/2) と真実 (真の表の出る確率) の乖離が大きいほど、仮説は棄却されやすい、つまり有意になりやすいことがわかりました。
一旦整理
この時点で 3 種類の確率が出てきているので整理しましょう。
コインの表の出る確率
検証対象の仮説ではずっと 1/2 という値になるとしてきました。上で議論した 3 つのシナリオでは、0.51、0.6、0.9 の値を考えました。
p 値
p 値も確率でしたよね。具体的には、仮説が正しい場合に、手元のデータと同等かそれ以上に珍しいデータが得られる確率です。「仮説が正しい」という仮定下において計算しているのがポイントです。
検出率
ここで新しい用語が登場しましたが、これは上で計算したような、仮説が棄却される確率のことです。ただし p 値は仮説に基づいて計算されるものですが、検出率は真の値 (0.51 や 0.6、0.9 など) に基づいて計算されます。
サンプルサイズが大きければ有意になりやすい
引き続き以下の設定を考えていきます。
- 仮説:コインの表の出る確率は 1/2
- 有意水準:5%
コインの表の出る真の確率が 0.51 だったとしましょう。このコインを N 回投げて、棄却域に入る確率を表にすると以下のようになります。
| サンプルサイズ | 棄却域 | 検出率 |
|---|---|---|
| 100 | 39 以下 or 60 以上 | 0.03886132396202924 |
| 1000 | 468 以下 or 531 以上 | 0.09119230707450587 |
| 10000 | 4901 以下 or 5098 以上 | 0.5120312250976096 |
100 回投げたときの検出率は前節でも見た通り 4% 弱です。しかし投げる回数を増やすと、検出率が大きくなることが見てとれます。10000 回投げると、50% を超える確率で仮説が棄却できることになります。
たとえ仮説と真実の乖離がほんのわずかであったとしても、サンプルサイズを大きくすることさえできれば、仮説を棄却することも思いのままです。
検定を何度も行えば有意になりやすい
5% の確率で当たるクジを考えましょう。このくじを 1 回引いたとき当たる確率はいくらでしょうか。当然ながら 5% ですね。
では 2 回引いたとき、少なくとも 1 回当たる確率はいくらでしょうか。これは 9.8% ほどです (余事象の確率を思い出そう!)。
では 10 回引いたとき、少なくとも 1 回当たる確率はいくらでしょうか。これは 40% を超えます。
有意水準を 5% に設定した検定を考えます。上でも説明したように、α エラーを引き起こす確率は有意水準に等しく 5% です。したがってクジの話は以下と同等です。
- 検定を 1 回行ったとき、α エラーを引き起こす確率は 5%。
- 検定を 2 回行ったとき、少なくとも 1 回 α エラーを引き起こす確率は 9.8% ほど。
- 検定を 10 回行ったとき、少なくとも 1 回 α エラーを引き起こす確率は 40% 以上。
多重検定
つまり、各検定で α エラーを引き起こす確率を 5% に設定していたとしても、複数回の検定全体においては α エラーを引き起こすリスクが増大するということです。これを検定の多重性や多重検定の問題などと言います。
例えば以下のような手続きが多重検定にあたります。
- まずはシンプルに分析してみよう。有意差が出ないなあ。
- 次は性別を考慮に入れて分析してみよう。これも有意差が出ないなあ。
- 次は年齢も考慮に入れて分析してみよう。今度は有意差が出た。これで論文が発表できるぞ。
Web サイトの A/B テストでよくある多重検定は以下のようなパターンでしょうか。データが集まるたびに検定を行い、有意差が出たタイミングで終わらせるというのは典型的な多重検定です。本当は施策になんの効果も無いはずなのに、効果があると誤った結論を出してしまう可能性が高くなってしまいます。
- A/B テストスタート!数日後に様子を見てみよう。
- 3 日後:有意差出てるかな。もしそうならテスト終わらせてもいいんだけどな。まだっぽいな。
- 4 日後:有意差出てるかな。もしそうならテスト終わらせてもいいんだけどな。まだっぽいな。
- 5 日後:有意差出てるかな。もしそうならテスト終わらせてもいいんだけどな。まだっぽいな。
- ...
有意差があっても差があるとは限らない
有意差というのは言うなれば統計的な差です。それがビジネス的に意味があるかはまた別の話です。ここではビジネスと言いましたが、医療などでも同様ですね。
上で、サンプルサイズさえ大きくすれば、どんな小さな差であってもあぶり出すことができることを説明しました。コインの表の出る確率が 0.5 なのか、それとも 0.51 なのかがどれほど重要かは場合によります。スポーツの先攻後攻に利用されるのなら、「意味のある差」かもしれませんし、友達と買い出し担当を決めるくらいなら「意味のない差」かもしれません。
あくまで有意かどうかは統計的 (ないしは確率的) に意味があるかを示しているにすぎません。それが現実世界で意味があるかはまた別の話です。
p-hacking
一般には p 値が小さいほうが嬉しいものです。たとえば現行の薬と新薬を比較するとします。通常は、両者に差が無いという仮説を考え、データによってその仮説を棄却することを目標にします。
p 値が小さければ (とくに有意水準を下回れば)、両者に差があるということになり、論文を出すことができたりビジネスが進んだりするわけです。
となれば検定者には、p 値を小さくなるようにするインセンティブが自然と生まれます。p 値が小さくなるようなデータだけを選んだり、後から検定手法を変えたりなどすることを p-hacking (p 値ハッキング) と呼びます。一言で言えばズルです。多重検定もその一つですね。
以下のような鋭い指摘を思いついた方もいるかもしれませんが、これはこれで解決すべき課題ですね。現状は研究者倫理に委ねられていると言えるでしょう。
- 有意差が無いと論文として認められないのがおかしい
- 簡単にズルができてしまう統計的仮説検定というフレームワークにも問題がある
ASA 声明
これまで説明してきた統計的仮説検定は、とても難しいフレームワークです (難しいなと感じているのならそれは真っ当な感想です)。とくに p 値という概念について勘違いされていたり、間違った使い方をされていたりすることがよくあります。プロの研究者でさえうまく使いこなせておらず、ASA (アメリカ統計協会) が声明を出すほどです。
ASA 声明 (日本語訳 には以下のようなことが書かれています。興味のある方は全文読んでみてください。
- p 値は仮説が正しい確率ではない
- p 値が 2.1% というのは、仮説が正しい確率が 2.1% という意味ではありません。
- ここまで説明してきた統計の枠組みでは、仮説が正しい確率というようなものをそもそも考えることができません。
- 気になる人は頻度論とベイズ論の違いとかで調べてみてね!
- 検定手続きのすべてを報告すべき
- 有意差が出た検定だけを報告してしまうと、査読者は多重検定が行われたことすら分かりませんよね。
- 多重検定だけが問題なわけではないですが、検定プロセスをすべて公開し、透明性を高くすることが重要だということです。
- p 値や統計的有意性は、効果の大きさや結果の重要性を意味しない
- 統計的に有意だからといってビジネス的に意味があるとは限らないことについて上で説明しましたね。
- 他にも、p 値が極めて小さいためはっきりと差がある、みたいな論調も間違いです。
- p 値以外も活用すべき
- 信頼区間やベイズファクターなど、より良い指標を使うことも考えたいですね。
- ただ、さらに統計学の深いところへと踏み込むことにはなりますが...。
まとめ
確率を使うことで、仮説が正しいかどうかを定量的に測ろう、というのが統計的仮説検定の考え方です。しかし確率を使うがゆえの難しさがあるというのがわかりました。なかなか一筋縄ではいかないんだなあというのを感じていただけてたと思います。
統計学は強力な道具ではありますが、決して万能ではなく、正しく使うことが大切なんだということを理解していただれば幸いです。