はじめに
統計的仮説検定のコアコンセプトを具体例を使って解説しました。本文中に数式 (数学 A の反復試行の確率) が出てきますが、飛ばしながらでも読めるようになっています。
まずは感覚的に
統計的仮説検定とは、得られたデータが仮説を支持するものかどうかを、統計的な観点から判定する方法論のことです。早速具体例を見ていきましょう。
手元に 1 枚のコインがあるとします。このコインについて次のような仮説を考えていきます。
仮説
コインの表の出る確率は 1/2
つまり表と裏の出る確率が等しいという仮説を考えています。スポーツの先行後攻を決めるために使うコインであれば、出る面に偏りがあっては困りますからね。このようなコインを公正なコインと言ったりします。
さて、これを検証する方法はいくつかありそうです。例えばコインの寸法を計測し、歪みや偏りが無いことを確認すれば、公正なコインであると結論づけることができるかもしれません。
一方で統計的な検証というのは、データを収集し、そのデータを評価することで行われます。当然そのためにはデータが必要なので、コインを何回か投げて表の出た回数を記録してみましょう。
例えば 10 回投げて 4 回だけ表が出たとします。このデータは仮説を支持するものでしょうか、それとも仮説を否定するものでしょうか。
仮説が正しい場合、つまり表と裏の出る確率が等しい場合でも、10 回中 4 回しか表が出ないというのも全然ありえそうです。
次に 100 回投げてみたところ、40 回だけ表が出ました。100 回中 40 回だけとなると、仮説は成り立たなさそうに感じますね。
では 1000 回中 400 回だけ表が出たとしたらどうでしょう。さらに仮説を否定したくなりますね。
ここまでは「ありえそう」や「否定したくなる」のような曖昧な表現をしてきましたが、確率を使うことで定量的かつ厳密に議論することができます。
確率の計算
検定プロセスを理解するために、まずは「10 回投げてすべて裏だった場合」を考えましょう。仮説検定の主要なステップのひとつは、仮説が正しいと仮定したときに、10 回すべてが裏となるのはどれほど珍しいことなのかを計算することです。
ここでちょっとテクニカルな注意点があります。今、コインの表と裏が等確率で出るかどうかを考えていて、特に表と裏に区別はありません。表のほうが出やすい場合と、裏のほうが出やすい場合とでは、仮説を否定するという意味で違いはないということです。場合によっては区別することもあるのですが、ここでは深入りしないことにします。
このような扱いであるため、「10 回すべてが裏となるのがどれほど珍しいか」は以下のように計算します。
これは以下のグラフのグレー背景の部分の面積の和に対応します。
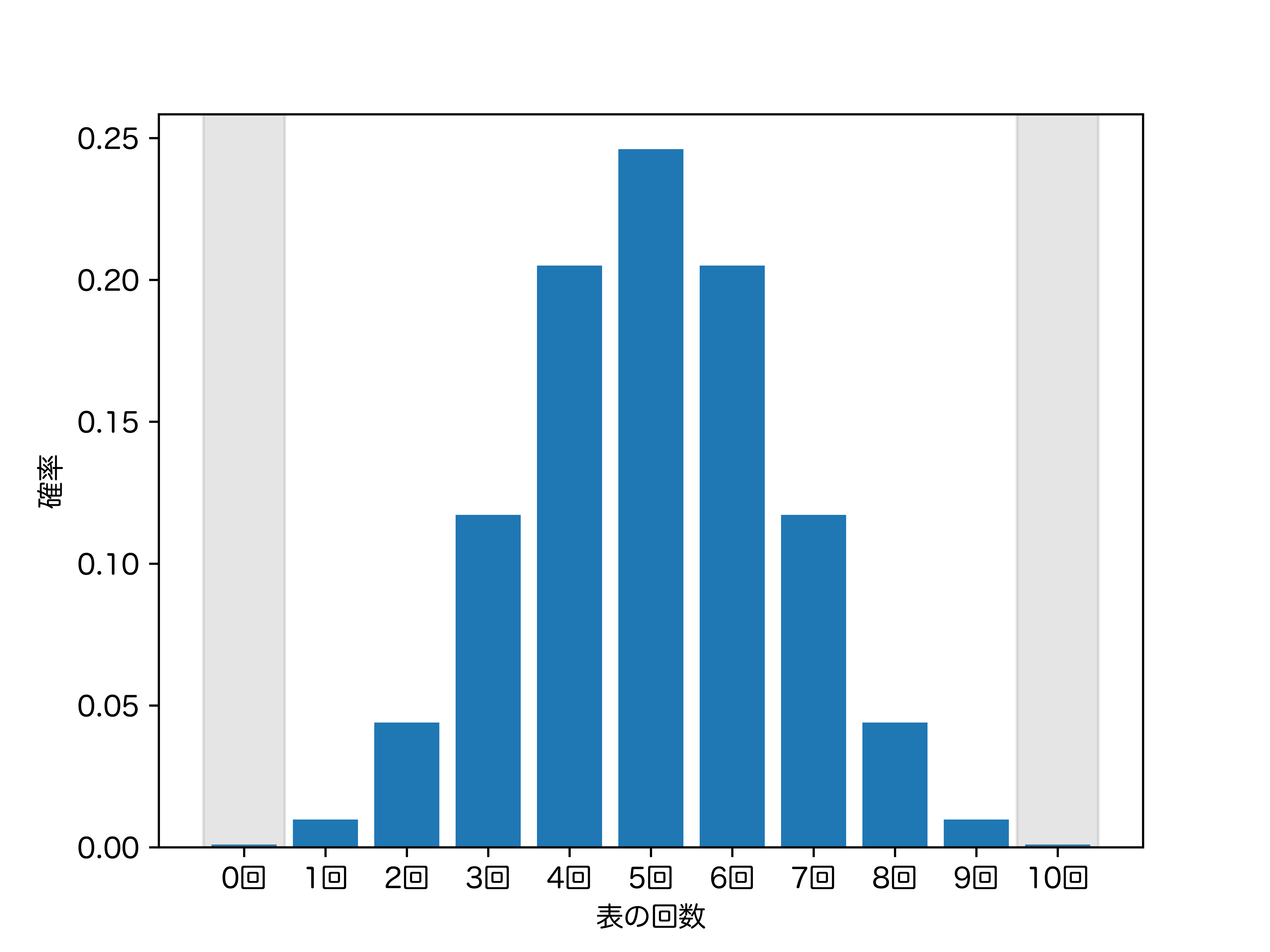
計算結果はだいたい 0.2% です。
もし仮説が正しいのだとしたら、これほどまでに珍しい現象が起こるというのは道理にかないません。つまり、「10 回すべてで裏が出た」というデータは仮説を否定することになります。
次に 10 回中 1 回だけ表が出たとします。このとき、仮説が正しい仮定したときにこのデータがどれほど珍しいかは次で計算します (反復試行の確率を思い出そう!)。
表と裏を区別していないので、10 回中 1 回だけ表が出た場合だけでなく、10 回中 1 回だけ裏が出た場合も含めるのはさっきと同様です。さらにそれだけではなく、10 回すべてが同じ面となる場合も含めているのがポイントです。「手元のデータほどの珍しいことが起こるのはどんな確率か」を計算しているためです。
これは以下のグラフのグレー背景の部分の面積の和に対応します。
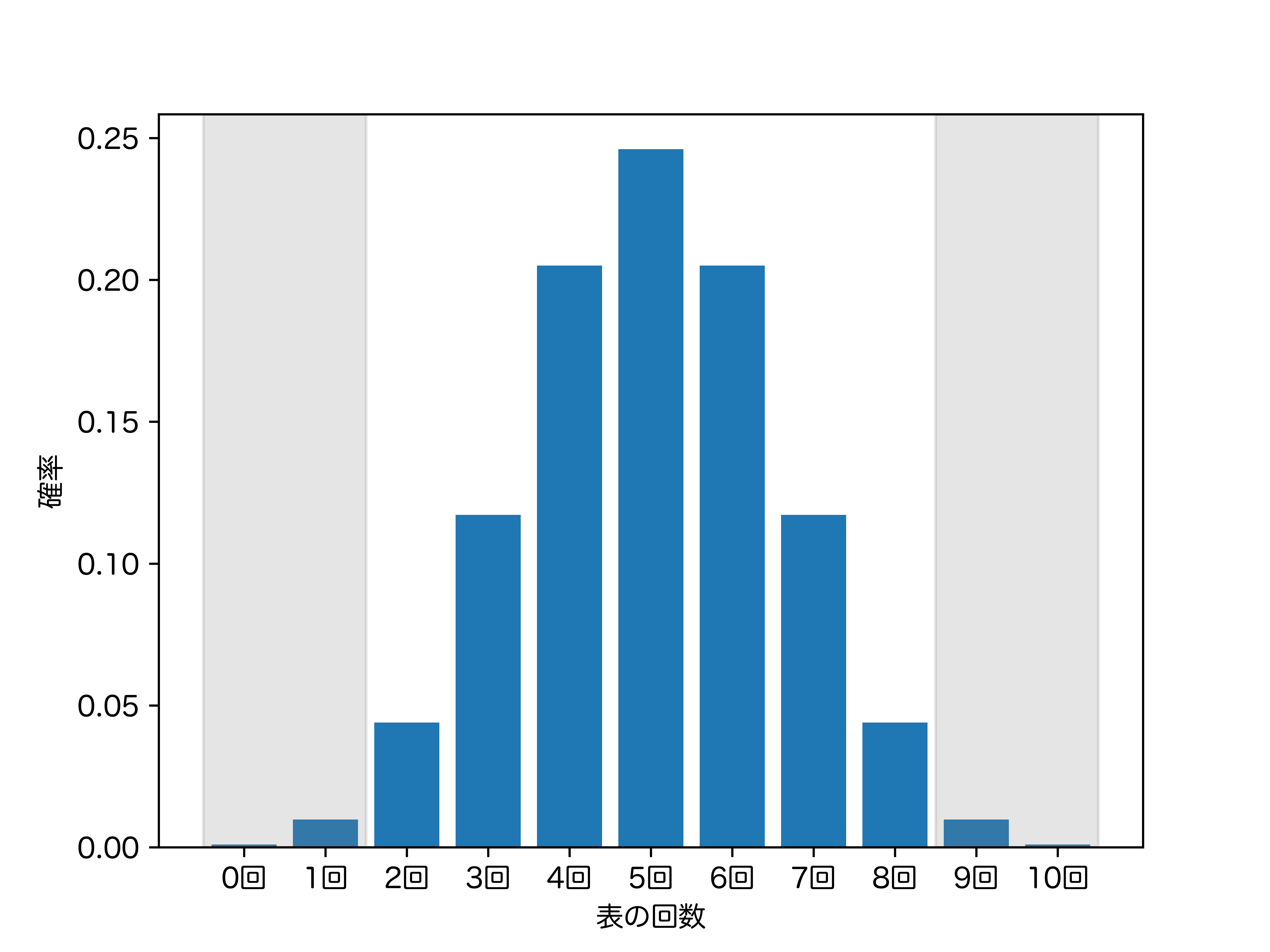
計算結果はだいたい 2.1% です。これも十分珍しいですね。
では次に、10 回中 4 回だけ表が出た場合を考えます。計算はこれまでと同様で、だいたい 75.4% と分かります。10 回中表が 4 回出るくらいなら全然ありえそうと述べましたが、それが定量的にも表現されました。
ちなみに 10 回中 5 回だけ表が出た場合、100% となります。つまり表と裏の出る確率が 1/2 である場合、コインを 10 回投げて表がちょうど 5 回出るのはなんら不思議ではない、ということです。
有意水準
厳密な議論をすると言っていたのに、珍しさの基準が曖昧だったことに気づいたでしょうか。0.2% は珍しいが 75.4% は珍しくない、と上で説明しましたが、そのボーダーラインはどこにあるのでしょうか。
このボーダーラインのことを有意水準と呼ぶのですが、なんと有意水準は自分で決めることができます。とは言ってもよく使われるのは 5% や 1% ですね。ただ、慣習的にこれらの数字が使われているだけで、明確な根拠があるわけではありません。
100 回投げた場合
次に 100 回中 40 回だけ表が出た場合で考えてみましょう。これまでと同様に、仮説が正しいと仮定したときにこのデータが得られることがどれほど珍しいのかは次で計算できます (反復試行の確率をもっと思い出そう!)。
手計算するのは骨が折れるので、コンピュータの力を借りて計算してみました。計算結果はだいたい 5.7% でした。
珍しさのボーダーラインである有意水準を 5% に設定していたとしたら、5.7% はそれよりも大きいため、このデータでは仮説を否定できないということになります。
用語の整理
ここで用語を導入・整理しておきましょう。
有意水準
何 % 以下を珍しい事象だとするか、というボーダーラインで、5% や 1% がよく使われます。自分で決めることができますが、事前に決めておきましょう。事前にというのは、ズルにならないように、ということです。例えば 1% では有意 (下で説明) にならなかったから、やっぱり有意水準を 5% に変えよう、などとしてはなりません。
p 値
仮説が正しいと仮定したときに、手元のデータがどれほど珍しいものかを表す確率値です。もう少し厳密に言うと、仮説が正しいと仮定したときに、手元のデータと同等かそれ以上に珍しいデータが得られる確率です。上の例でも、「コインの表の出る確率は 1/2」という仮定のもとでは、「10 回中 4 だけ回表が出た」というデータは 75.4% の確率でありえるものだと計算しました。この 75.4% という数値が p 値です。
有意
p 値が有意水準を下回ることです。どちらかというとデータに対して使う言葉です。例えば、有意な結果が得られた、のように使います。
棄却
p 値が有意水準を下回ったということは、仮説を否定する証拠が得られたということです。その場合、仮説は棄却された、というような言い回しをします。
以下はすべて同じ意味であることを補足しておきます。
- p 値が有意水準を下回る
- 結果が有意である
- 仮説が棄却される
棄却域
次のような設定を考えます。
- 有意水準を 5% で考える
- コインの表の出る確率が 1/2 であるという仮説を、コインを 10 投げることで検定する
このとき、仮説が棄却されるような表の回数を、棄却域と言います。
例えば、表 (おもて) の各回数に対する p 値は以下の表 (ひょう) のようになります。
| 表の回数 | p 値 |
|---|---|
| 0 | 0.2% |
| 1 | 2.1% |
| 2 | 10.9% |
| 3 | 34.4% |
| 4 | 75.4% |
| 5 | 100% |
| 6 | 75.4% |
| 7 | 34.4% |
| 8 | 10.9% |
| 9 | 2.1% |
| 10 | 0.2% |
有意水準を 5% に設定していますから、表の出る回数が 0、1、9、10 回のとき、仮説は棄却されることとなります。つまりこの場合は 0、1、9、10 が棄却域です。これは以下のグラフのグレー背景の部分に対応します (さっきも同じ画像をあげましたね)。

100 回投げる場合は、以下のように 39 回以下もしくは 61 回以上が棄却域となります。棄却域は有意水準を設定して初めて決まるものであるということに注意しましょう。
| 表の回数 | p 値 |
|---|---|
| 38 | 2.1% |
| 39 | 3.5% |
| 40 | 5.7% |
| ... | |
| 60 | 5.7% |
| 61 | 3.5% |
| 62 | 2.1% |
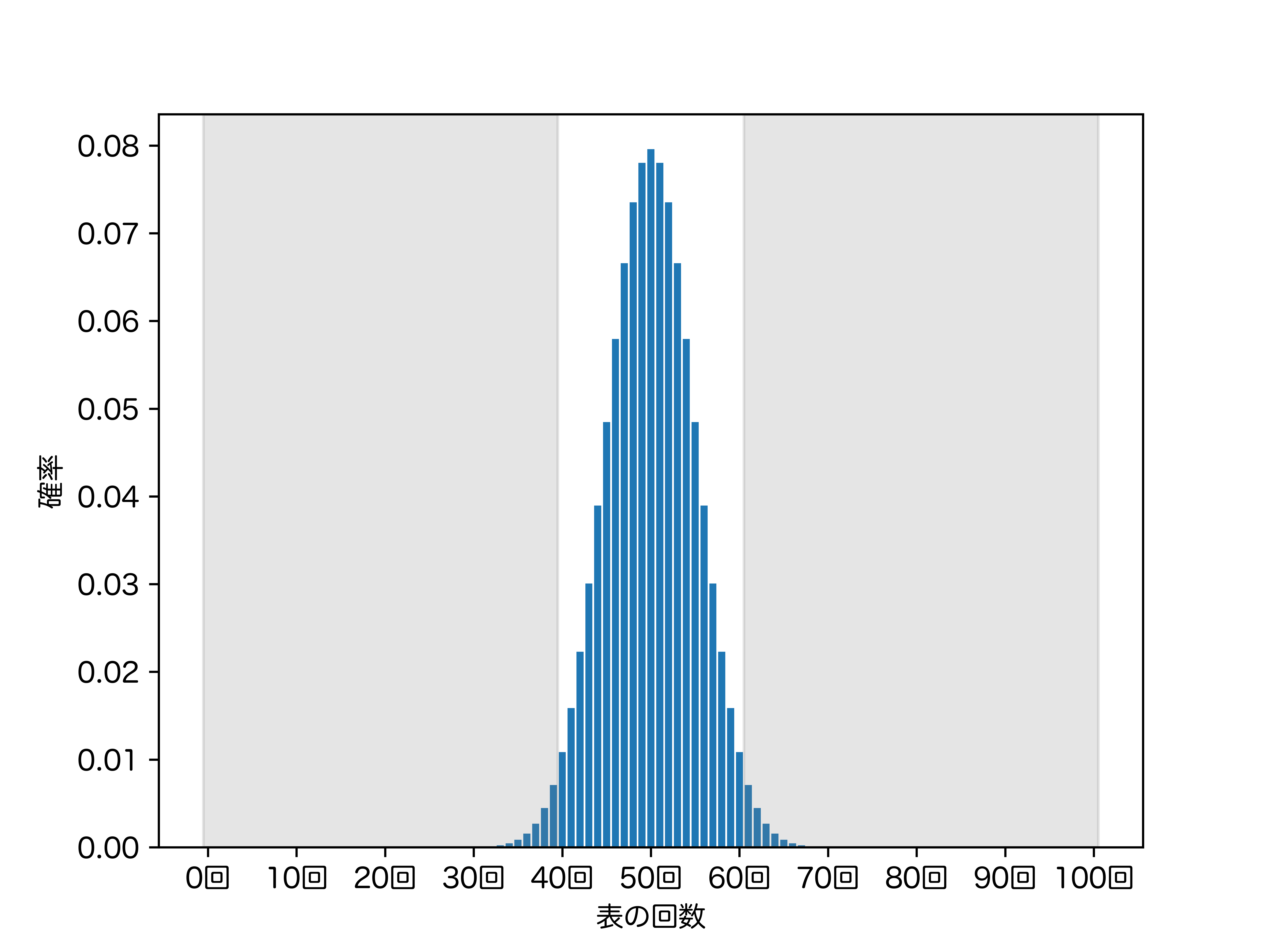
サンプルサイズ
データ量のことです。10 回コインを投げた場合はサンプルサイズが 10 で、100 回コインを投げた場合はサンプルサイズは 100 です。
おおまかなプロセス
最後に、統計的仮説検定のおおまかなプロセスを説明します。
| ステップ | 例 |
|---|---|
| 仮説を立てる | 手元のコインは公正である |
| サンプルサイズや有意水準を決めておく | コインを投げる回数は 100 とし、有意水準は 5% とする |
| データを集める | 100 回コインを投げて、表と裏の回数を記録する |
| p 値を計算する | 表の回数が 40 である場合の p 値は 5.7% |
| 結論を出す | p 値が有意水準を下回らなかったため仮説は棄却されない |
まとめ
統計的仮説検定のコアコンセプトと、ベーシックな用語について解説してきました。統計的仮説検定の雰囲気はつかめたでしょうか?
あらゆる領域で使われている仮説検定ですが、実践するのは簡単ではなく、注意すべき点も多くあります。それについてはまた別の記事で解説することにしましょう。